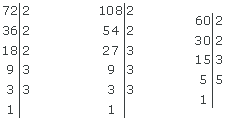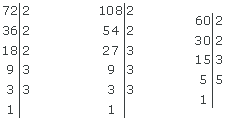Sistema de numeración 12
Llamado El sistema duodecimal
Es un sistema de numeración posicionar usando la notación de doce como su base. En este sistema, el número diez se puede escribir como "A", "T" o "X", y el número once como "B" o "E" para diez y un invertido "3" para once). El número doce se escribe en lugar de "10" en duodecimal, mientras que la cadena de dígitos "12" significa "1 decena y 2 unidades." Del mismo modo, en duodecimal "100" significa "1 gross", "1000" significa "1 gran bruto", y "0.1" significa "1 duodécimo".
Ejemplo:
Sistema de Numeración 16
Llamado como El sistema hexadecimal
(a veces abreviado como Hex, no confundir con sistema sexagesimal) es el sistema de numeración posicional que tiene como base el 16. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria
tabla de multiplicación
En el sistema hexadecimal, al igual que en el sistema decimal, binario y octal, se pueden hacer diversas operaciones matemáticas.
Entre ellas se encuentra la resta entre dos números en sistema hexadecimal, la que se puede hacer con el método de complemento a 15 o también utilizando el complemento a 16.
Además de éstas, debemos manejar adecuadamente la suma en sistema hexadecimal
| Hexadecimal | Decimal |
|---|
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F |
15
|
Suma
- 9 + 7 = 16
- (16 - 16 = 0 nos llevamos 1 y es = 10 )
En este caso la respuesta obtenida, 16, no está entre el 0 y el 15, por lo que tenemos que restarle 16. Por lo tanto, la respuesta obtenida será 10 (sistema hexadecimal).
Hay que tener cuidado de utilizar correctamente las letras, ya que operar a la vez con letras y números puede crear confusiones.
Resta
Como podemos hacer la resta de dos números hexadecimales utilizando el complemento a 15.
Para ello tendremos que sumar al minuendo el complemento a quince del sustraendo, y finalmente sumarle el bit de overflow (bit que se desborda).
Para entender la resta en complemento a 15 lo analizaremos con un ejemplo. Ésta es la resta que tenemos que resolver:
A4FC9
- DE8
—————————
¿?¿?¿?¿?
Sistema de Numeración 20
Llamado tambien como Un sistema vigesimal
Es un sistema numérico, para nombrar los números y contar, basado en el número veinte. Este sistema de numeración, junto con el sistema decimal, se halla extendido por casi todo el planeta.
El sistema de numeración decimal, también llamado sistema decimal, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética las potencias del númerodiez
Excepto en ciertas culturas, es el sistema usado habitualmente en todo el mundo y en todas las áreas que requieren de un sistema de numeración.
SISTEMA DE NUMERACIÓN 60
Llamado también El sistema sexagesimal
es un sistema de numeración posicional que emplea como base aritmética el número 60.
Tuvo su origen en la antigua Babilonia. También fue empleado por los árabes durante el califatoomeya. El sistema sexagesimal se usa para medir tiempos (horas, minutos y segundos) y ángulos (grados, minutos y segundos).
El número 60 tiene la ventaja de tener muchos divisores (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60), con lo que se facilita el cálculo con fracciones. Nótese que 60 es el número más pequeño que es divisible por 1, 2, 3, 4, 5 y 6.
SUMA Y RESTAS
El sistema sexagesimal es un sistema de numeración en el que cada unidad se divide en 60 unidades de orden inferior, es decir, es su sistema de numeración en base 60. Se aplica en la actualidad a la medida del tiempo y a la de la amplitud de los ángulos.
Suma
PRIMER PASO
Se colocan las horas debajo de las horas (o los grados debajo de los grados), los minutos debajo de los minutos y los segundos debajo de los segundos; y se suman.
SEGUNDO PASO
Si los segundos suman más de 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirá a los minutos.
TERCER PASO
Se hace lo mismo para los minutos.
Resta
PRIMER PASO
Se colocan las horas debajo de las horas (o los grados debajo de los grados), los minutos debajo de los minutos y los segundos debajo de los segundos.
SEGUNDO PASO
paso Se restan los segundos. Caso de que no sea posible, convertimos un minuto del minuendo en 60 segundos y se lo sumamos a los segundos del minuendo. A continuación restamos los segundos.
TERCER PASO
Hacemos lo mismo con los minutos.
SISTEMA DE NUMERACIÓN 64
Base 64
es un sistema de numeración posicional que usa 64 como base.
Es la mayor potencia de dos que puede ser representada usando únicamente los caracteres imprimibles de ASCII.
Esto ha propiciado su uso para codificación de correos electrónicos, PGP y otras aplicaciones.
Todas las variantes famosas que se conocen con el nombre de Base64 usan el rango de caracteres A-Z, a-z y 0-9 en este orden para los primeros 62 dígitos, pero los símbolos escogidos para los últimos dos dígitos varían considerablemente de unas a otras.
La primera aplicación conocida de la codificación Base 64 para transmisiones electrónicas de datos fue el protocolo Privacy-enhanced Electronic Mail (PEM)
(para todo…) se denomina cuantificador universal, y el símbolo 
(existe al menos un…) se denomina cuantificador existencial. 
(existe un único…): se utiliza para indicar que existe exactamente un elemento en el conjunto A que cumple con una condición o propiedad determinada.
